Verify the Calculations for the Autocorrelation Function of an Arma(1, 1) Process Given

For an ARMA(1, 1) process

Now let's suppose that |φ ₁| < 1. We show how to create the MA(∞) representation as follows:

Thus

whereψ ₀ = 1 and for j > 0

The MA(∞) representation is therefore

If |φ ₁| < 1, then this ARMA(1,1) process is stationary. It also turns out that when |θ ₁| < 1, the process is invertible.

Example 1: Find the MA(∞) form of the ARMA(1, 1) process y _i =.4y _i-1 +ε_i – .2ε_{i -1}

etc.

We get the same result using the Real Statistics PSICoeff array function as shown in Figure 1.

Figure 1 – Finding MA(∞) Coefficients

Property 1: The following is true for an ARMA(1,1) process

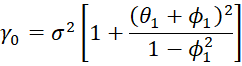
Proof: See ARMA Proofs

Property 2: The following is true for an ARMA(1,1) process

and for k > 1

Proof:See ARMA Proofs

Observation: Sincez ₁ = 1/φ ₁ is the root of the characteristic polynomialφ(z) = 1 –φ ₁ z, we can express the second term in Property 2 as

It turns out that this can be generalized to other ARMA processes.

Property 3: The following is true for an ARMA(1, 1) process

and for k > 1

Proof: See ARMA Proofs

Observation: When θ ₁ = –φ ₁ for an ARMA(1, 1) process, we note that γ ₀ = σ ² and ρ_k = 0 for all k > 1, which are the characteristics of white noise.

In fact, the white noise process with zero mean takes the form

y _i = ε_i

We see that φ ₁y _i  – φ ₁ε_i = 0  for all i, and in particular φ ₁y _{i- 1}  – φ ₁ ε _i-1 = 0. Thus, the process takes the form

which is an ARMA(1,1) process with θ ₁ = –φ ₁.

Example 2: Simulate a sample of 105 elements from the ARMA(1,1) process

where ε_i ∼ N(0, 1) and calculate the ACF.

This is done in Figure 2 by placing the formula =NORM.S.INV(RAND()) in cell B7 and the formula =0.7*C6+B7-0.2*B6 in cell C7, highlighting the range B7:C111 and pressing Ctrl-D (only the first 16 elements of the simulation is shown in Figure 2).

Figure 2 – Simulated ARMA(1,1) process

The ACF values are shown in Figure 3 where the theoretical values are based on Property 3.

Figure 3 – ACF for ARMA(1,1) Process

Cell M6 contains the formula =ACF($C$12:$C$111,L6), and similarly, for the other cells in column M, cell N6 contains the formula =(Q5+Q6)*(1+Q5*Q6)/(1+2*Q5*Q6+Q5^2) and cell N7 contains the formula =N6*Q$5, and similarly for rest of the cells in column N.

Since |φ ₁| = .7 < 1 and |θ ₁| = .2 < 1, this process is both stationary and invertible.

Example 3: Simulate a sample of 105 elements from the ARMA(1,1) process

where ε_i ∼ N(0, 1) and calculate the ACF.

The only difference between this process and the one in Example 2 is the constant term. The approach is identical, except that this time you place the formula =3+0.7*C6+B7-0.2*B6 in cell C7. The result is shown in Figure 4. Note that the ACF values are identical to those in Figure 3.

Figure 4 – Simulated ARMA(1,1) Process with non-zero mean

Verify the Calculations for the Autocorrelation Function of an Arma(1, 1) Process Given

Source: https://www.real-statistics.com/time-series-analysis/arma-processes/arma11-processes/

Share this post